沪icp备2021017797-1 沪公网安备 31010902003140号
Copyright @ 2006-2024 上海高顿教育科技有限公司 All Right Reserved
【思路】
总共100人，平均分是86.2，那么总分是8620分。有70%的学生成绩不低于70分，即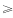
70分的人数为70人，则成绩
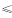69分的人数为100-70=30人。因为70
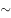75分低于总平均分86.2分，所以要想让成绩在70-75分的人数最多，则低于70分的学生成绩要尽可能靠近70分，最大能取到69分，即低于70分的30人得分均为69分。假设不低于70分的70人中，成绩在70-75分中有x人，每人得分是y（70≤y≤75）。要使70-75分的人尽可能多，则要使剩下的70-x人分数尽可能高，即每人得100分。由此可列方程30×69+xy+（70-x)100=8620，化简得x=450/（100-有），x越大，x越大，当y取最大值75时，x最大，为450/（100-75）=18人。
因此，答案为A。
常见问题
查看更多>
相关文章推荐
查一查
我能报考什么职位?
全国
请选择类型
一键查询合适岗位
