沪icp备2021017797-1 沪公网安备 31010902003140号
Copyright @ 2006-2024 上海高顿教育科技有限公司 All Right Reserved
【思路】
概率问题。根据公式
，本题有两种解题方法。方法一：根据题意可知，总的等可能样本数为10人围绕圆桌就坐的全部情况，则
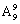种方法；则5对夫妇恰好都被安排在一起相邻而坐，即5对夫妇捆绑后环形排列，则有
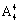种方法，每对夫妇内部有2种排列方法，则5对夫妇相邻而坐的总方法数为
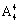×2×2×2×2×2=
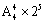种方法，则
=
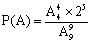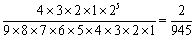
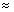2‰。
方法二：本题可用分步概率求解。从10人中任意选择1人坐下后，其余9人中其配偶的概率为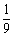
；再任意选取一人坐下后，其余7人中其配偶的概率为
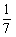；同理，第三对夫妻坐在一起的概率为
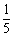；第四对夫妻坐在一起的概率为
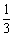；第五对夫妻坐在一起的概率为
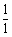=1，则5对夫妇恰好都被安排在一起相邻而坐的概率
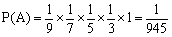，由于环形排列包括顺逆2种情况，则总的概率为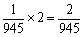
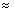2‰。
因此，答案为A。
常见问题
查看更多>
相关文章推荐
查一查
我能报考什么职位?
全国
请选择类型
一键查询合适岗位
